遞迴最小二乘、卡爾曼濾波與配對交易 - 地球科學系二年級 張育誠

課程名稱►遞迴最小二乘、卡爾曼濾波與配對交易 授課教師►數學系 許瑞麟老師
心得分享者►地球科學系三年級張育誠
選修動機:
我不是第一次修習模組化課程,因此對於新的密集課程較能夠適應。多次耳聞過數學系的許瑞麟教授非常致力於跨領域模組化課程的推廣,老師已經開課多年且在這種一周式的密集課程曾經扮演過學生的角色,學到許多後才自己開課的,因此許老師對密集課程的專業度非常高,懂得如何在很短的時間內將學習成果最大化。在M沙龍中許瑞麟老師的開課主題也是讓我最感興趣的,最有印象的是老師說過,選修模組化課程,最壞的結果僅僅是不感興趣。能有機會用一周的時間認知到自己對某方面沒興趣,比你直接填雙主修甚至轉系後才後悔,更適合拿來做跨域嘗試。再者你學到了這些跨領域基礎知識,未來才能夠和這方面的專家合作,才聽得懂他們之間的術語。在這幾次的模組化課程後,我印證了老師的這段話,放棄了一些不切實際的幻想,也開發了不少完全不是我專業卻很感興趣的內容。
回到課程本身,許瑞麟教授開設的是最小遞迴法與卡爾曼濾波再結合股票上的配對交易,這是一個非常廣的主題,因為很多領域的人都非常適合使用卡爾曼濾波的操作,關鍵在於會不會、懂不懂這項技術。更不用說配對交易,這是一項非常好的理財分析工具,因此我對這門課充滿了期待。
修課內容:
課程本身分為兩個部分:上午的教師講解單元內容與下午的助教帶領程式應用。上午的講課內容依序分成幾個大單元:Least square(LS)、Support vector machine(SVM)、Capital asset pricing model(CAPM)、Single index model(SIM)、Weighted least square(WLS)、Recursive least square(RLS)、Kalman filter(KF)與最後實際應用的Pairs trading,每個單元之間都有強烈的連結性,其中最重要的是第一天所教的LS之原理。首先我們要瞭解為甚麼需要用到least squares,我們可以先看到下面的圖片:

這邊講述的是當我們有四個相異不共線的點(m=4)而只有兩個未知數(n=2)時,我們就無法找到一條直線,可以同時通過給定四個點,得以預測當第五個點出現時可能會對應到的y值。最小平方法在找到一條直線,使得給定4點的誤差最小。但在現實中,此問題通常會變得極度複雜,可能是m=200000而n=6的狀態,那我們就不可能用手寫計算這個問題的最佳解,這就是為甚麼我們要學least squares的原因。而後面所教的WLS(加入權重)、RLS(加入遞迴預測)也都是Least squares的更深入延伸內容,可以模擬出更複雜的情況。
想當然的數學系所開設的課少不了數學證明,這也是課程評分的一大標準。雖然每天上完課程後會有1~2題當天所用公式的證明推導,但同學們也不用太擔心。作業的期限一般會是兩天,因此先回去操作後若真的做不出來也可以在隔天來詢問助教,助教們會適當地給予協助及提示。上午的教學課程主要的進行方式是教師準備當日ppt給同學們下載,上課過程中使用iPad連接投影幕形成類板書的形式,如此一來,若同學們對課程中有任何問題都可以直接提出後教師現場解決,非常便利!
每天下午課程是由助教們帶領同學進行程式實際操作,我認為這是非常好的課程規劃,在當天學完東西後可以馬上操作,實際感受自己到底在學甚麼東西。我們使用的是R語言,方便處理大量的統計資料,教學方式是助教先用一小時左右講解如何將上午學到的東西轉化為code的形式。要特別提到的是這邊並沒有要求先修程式語言的背景,助教們會當作大家完全沒有學過程式語言來一行一行解讀程式給同學們,因此不會程式語言的同學們也不用太擔心。你唯一需要先備的就是一台筆記型電腦!課程上助教會講解範例題目,並有少量的回家作業,和上課時的程式碼相似,若有認真上課的話應該都能在少少的時間內就完成了!單然助教們在下課後也很樂意留在班上幫大家解題,因此就算沒有程式背景甚至不是理工科系的同學們真的不用太擔心,別被課程名稱和數學系教授開設所嚇倒了!
接著我想要具體分享一下在程式實作的部分為什麼很吸引人。下圖是我們對微軟公司(MSFT)進行股價的預測,取用的數據是2019至2023年。
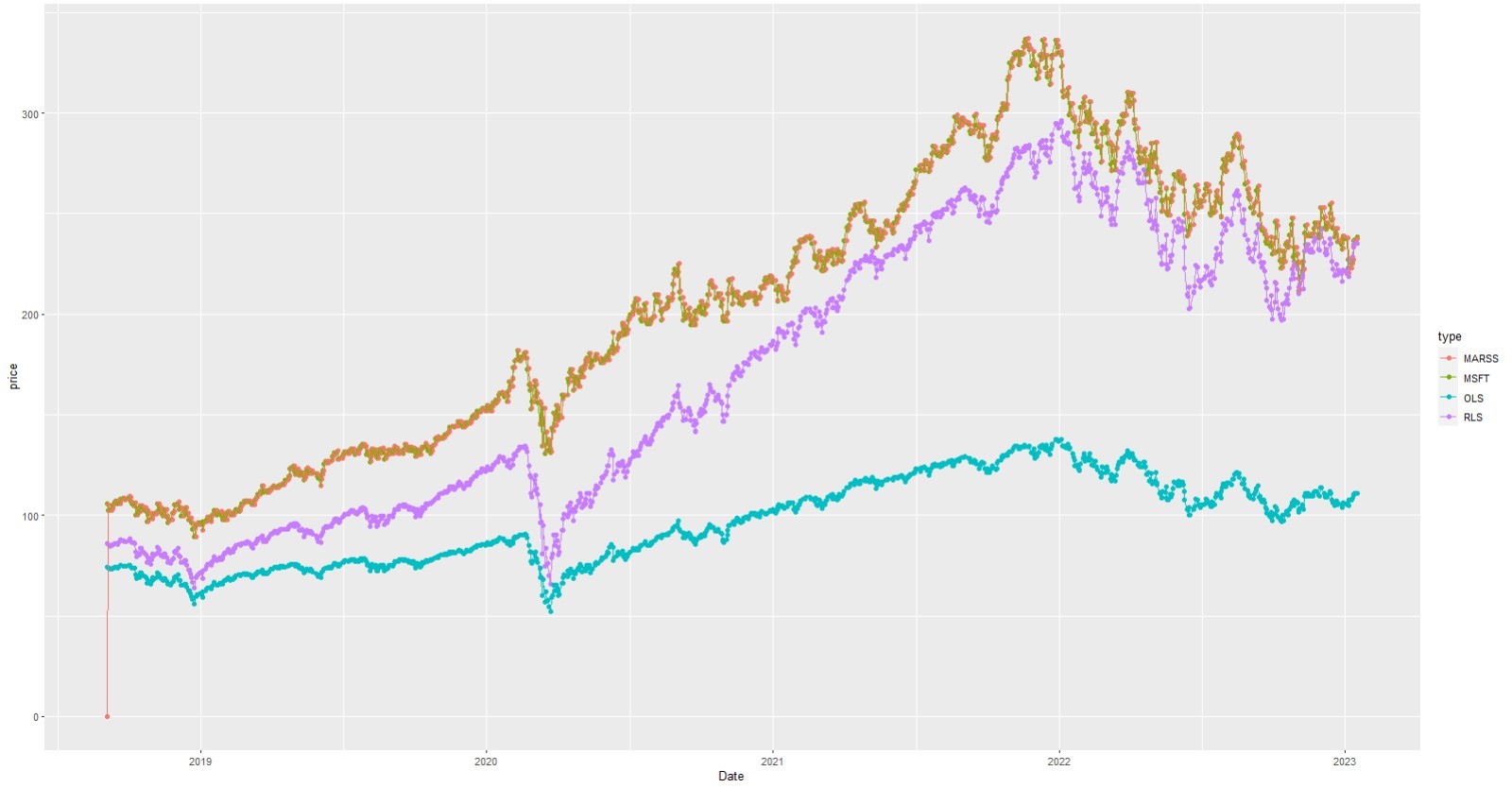
我們取用的是前面幾年的歷史股價數據,希望預測後面越接近現在的股價走勢。綠色的線是真的取出2019~2023年微軟股價的走勢圖,而藍色的線是最入門的least squares所繪製的走勢、紫色線是加入遞迴關係進行修正,而橘色線則是在遞迴上做多次迭代,融合權重等技術進行預測。我們發現橘色線幾乎和綠色的真實數據重疊,這也是這門課最吸引人的地方。
課程心得:
許瑞麟老師鼓勵大家多多嘗試跨領域、跳脫舒適圈,這門課也完全實踐了這件事。整個課程內容是非常龐大非常複雜的,更不用說還挪用了一半的時間做程式實作,因此在學習上總是會有些緊湊。然而最有趣的是自己的進步可以在程式實作中觀察到。除了學到R語言的基本操作外,也能讓預測結果日漸精準。課程給分的部分也很透明,大多是出席與作業成績為主。對於理工學系的同學們,可能較少能接觸到金融專業的機會,而學習金融或管理學系的同學則較少接觸到數學理論的機會,許瑞麟老師將兩者結合的非常融洽,使入門的門檻變得平易近人。只用五天的時間卻讓我發覺自己對金融部分有著一定的興趣,因此下學期我更勇於選修更多更深入的相關課程。鼓勵所有有意願學習新技能卻不敢跨出第一步的同學們,從模組化課程開始吧!
關鍵字 #成大模組化 #遞迴最小二乘法 #卡爾曼濾波 #金融結合程式 #配對交易


瀏覽數:
分享








