國立成功大學模組化課程

課程內容

這門課透過分析相異平衡方程式裡面的相同數學結構，解析不同領域所關注系統之平衡態，從而理解數學家常建構單一的數學模型，卻可以應用到不同的領域，使得我們能夠從不同的領域見到類似的數學結構。如果在學習一個的全新領域時，我們能利用類似的數學結構去思考並分析及學習，就能快速理解該領域大致的概念，達到跨域的目的。

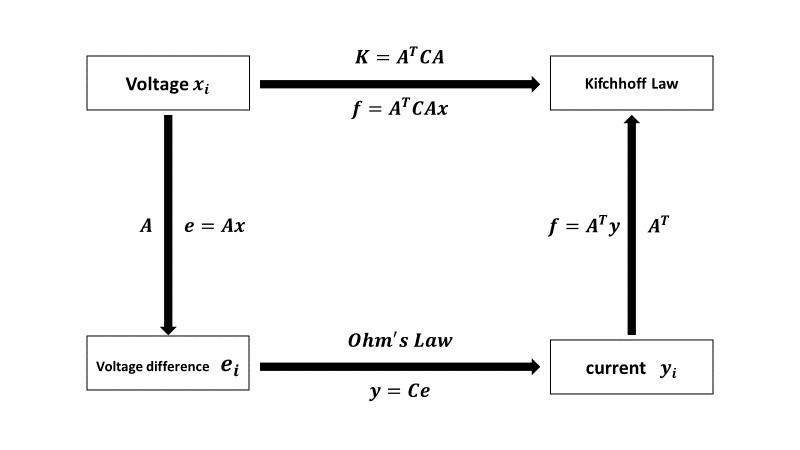
這門課首先從多個彈簧串聯的系統之震盪(一維的離散系統)出發，學習彈簧震動的平衡方程數學結構之形式，進而將此數學結構套用在連續的彈性棒(一維的連續系統)、電路系統(二維的離散系統)、以及平面的流體場(二維的連續系統)。隨著問題逐漸變得複雜，我們修正此數學結構的部份枝節，並引入一些額外的觀念，藉此解釋更為複雜的系統。而在電路系統中我們亦能將電流與電壓視為外加的物理量加入此系統，可透過分析得知兩者為分別加入node與edge上。

(下圖為此課程中最重要的數學結構)(Fundamental diagram)

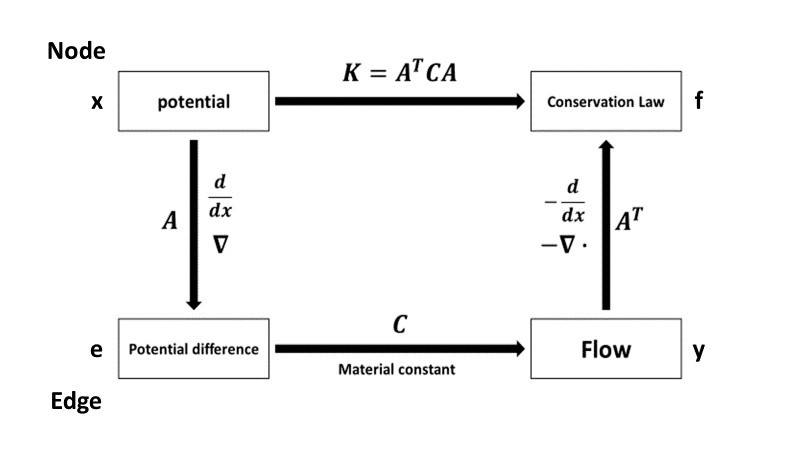
各理論與Fundamental diagram對應關係分別如下：

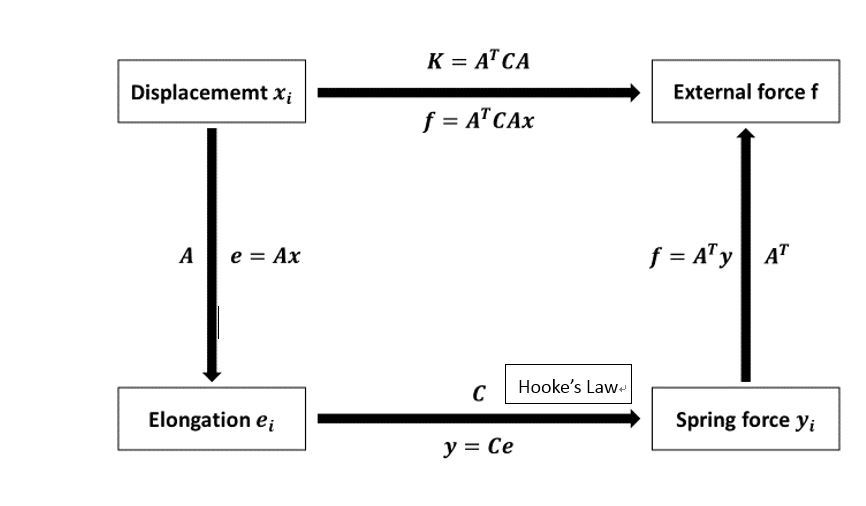
(1)一維的離散系統(一維彈簧系統)

(2)一維的連續系統(連續彈性棒)

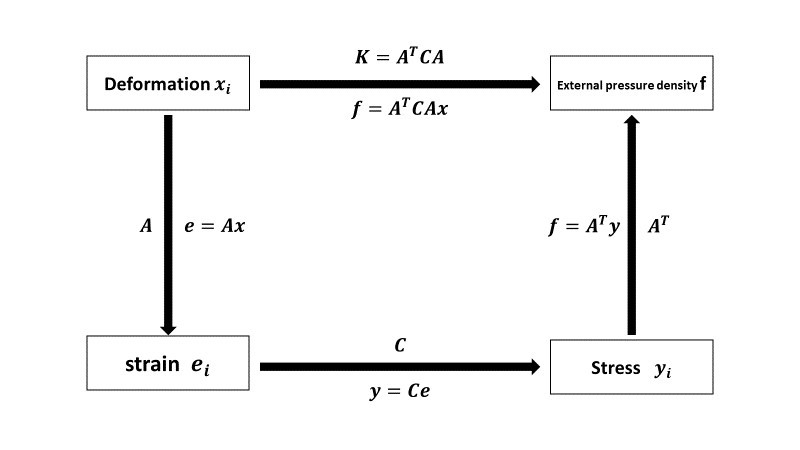
前述的兩個例子，最後都是用力平衡的觀點列出等式。

(3)二維的離散系統(電路系統)

(4)二維的連續系統(理想流體)

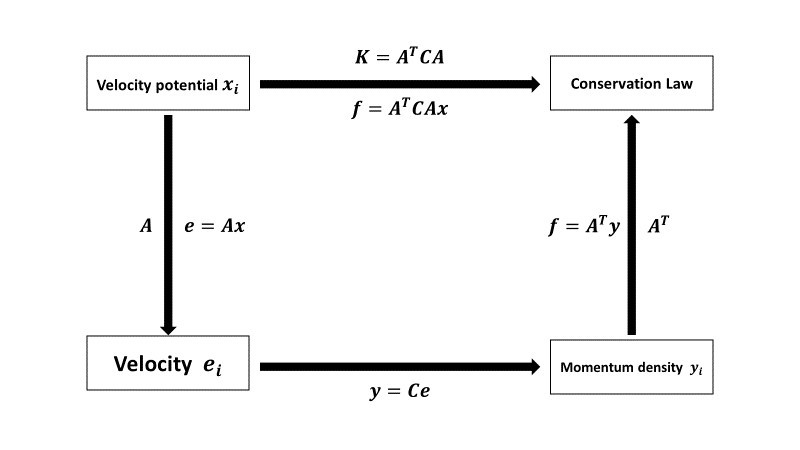
二維的連續系統用守恆率列式，就會得出Laplace equation。而藉由設定一單位圓為邊界條件後，我們能用Fourier Series展開求Laplace equation在這個邊界條件下的解。在課程的最後老師也介紹了Fourier Series的數學原理。

授課風格

這門課並不輕鬆，每天上課前都有一個小考，考前一天的上課內容。在課程最後也有一個心得報告。在課程進行中老師鼓勵同學問問題，會發一張黃卡，每次問問題後給老師或助教簽名，課程最後收回計分。

課程內容由淺入深，前面的兩個系統我覺得並不難，但到後兩個系統以我當時大一升大二來說就顯得吃力。尤其是最後許瑞麟老師花了許多時間在講解傅立葉級數、傅立葉轉換、線性代數解微分方程，這些部分我就非常吃力。但我還是從中擷取到一些實用的概念(在心得有詳加敘述)。整體來說我覺得許老師對於這些內容著墨頗深，有一些他個人的觀點，表達上也很容易能夠讓我接受到核心概念，這對我而言幫助很大。

課程進行中老師隨時可停下來讓學生問問題，也對學生的問題很重視的回應。授課時老師除了介紹課程內容外，也會聊一些關於自己為何要開設模組化課程、自己在貝爾實驗室的所見所聞、老師的朋友在國外的經歷、以及留學相關的事情、未來應具備的能力…等，這些在課程內容外的分享也對我自己有很深的影響。

心得

過去在物理上學習牛頓重力、電磁力時，時常會兩相對應，因為兩者所使用的是同一套數學，所以在物理概念的理解與數學式都能夠一一對應。而透過這門課我瞭解到背後其實有一套數學結構支撐整個對應的架構。雖然原本就知道能夠對應，但知道有這個數學架構後，可更加深自己對這架構的理解，並且清楚看到在不同領域各項對應的物理量為何，思考以及學習相同架構下的相關學說。

其實這些數學結構在歷史上的發展也相當有趣。當初向量分析是因為物理上電磁學的發展而在同時間建構起來之數學領域；而複變函數論、Hilbert space的數學發展也對應到量子理學的崛起。在歷史上物理理論時常會與建立其理論的數學理論同時建構起來。但我在授課時碰到了微分形式與積分形式的divergence theorem若且唯若的數學關係(∬_S ∇∙w dxdy = 0 ↔∇∙w=0)，但在物理上不論是在電磁學、流體力學都有這個關係的反例，所以我開始思考是否物理理論與數學理論必須完全對應。我得到的結論是並非如此。或許在物理上只要可以使用就好，並不是所有的物理理論都需要完全對應數學理論。(當然也是自己的數學能力不足，沒辦法去求證這項關係的證明，所以只能先暫時相信老師的說法。)

另外也學到所謂「函數內積」的概念，個人覺得非常新奇！過去其實有發現乘法在向量上分為內積與外積，只是為了決定兩個向量相乘後是否還是一個向量，所以自然有這兩種分類。而函數內積是把兩個向量分量相乘後每一項加起來的概念推廣，變成兩個單變數函數在x的值相乘後累加起來，也就是積分 ∫f(x)g(x)dx，這在直觀上非常容易理解，但在數學上據老師說需要非常嚴格的證明才會成立。

總結來說，這門課雖然與我物理的本科相關性較高，但讓我得以反思在這些理論背後的數學概念。過往我常將數學視為應用在物理上的工具，只要能使用即可。而在物理本科上，也有許多人因為數學本身的晦澀難懂，使得物理的理解上出現問題。經過這門課讓我意識到數學有其本質上的邏輯，依循這個邏輯能夠在學習物理的路上少走許多冤枉路，另一方面也能避免學物理卻被數學綁架的情形發生。

關鍵字#成大模組化#物理#Fourier Series#函數內積#平衡方程式